[BOJ] 11727 - 타일링2 (C++)

1. 알고리즘

DP문제로, 2*n은 이전 타일 붙여 나아 가면서 개수를 구할 수 있는 방식이다. 즉 큰 것을 구하기 위해 작은 단위부터 더해 나아가는 방식.. 

2. 전체 소스

2*n 타일은 2*n-1 번째의타일에서 2*1의 타일을 붙이는 값 더하기 2*n-1번째의 타일에서 2*2와 2*1 타일을 붙이는 값을 더해서 구할 수 있다.
arr를 선언하여 각 n번째 타일의 채운 가짓수를 저장한다.

#include <iostream> using namespace std; int arr[1001]; int main() { int n; cin >> n; arr[0] = 1; // n = 1일때 타일을 붙일 수 있는 개수 arr[1] = 3; // n = 2일때 타일을 붙일 수 있는 개수 for (int i = 2; i <= n+1; i++) { arr[i] = arr[i - 1] + 2 * arr[i - 2]; arr[i] %=10007; } cout << arr[n-1] << endl; return 0; }

3. 참고 사항

이문제는 알고보면 굉장히 간단한 문제임에도 불구하고 시간초과, 틀렸습니다의 결과를 보게 되었다. 
시간 초과에 관련된 소스는 아래 5번 틀린문제에 있는데 이건 안봐도 되는 소스.. 너무 복잡하게 생각해서 구현했더니 시간 초과가 발생했다.
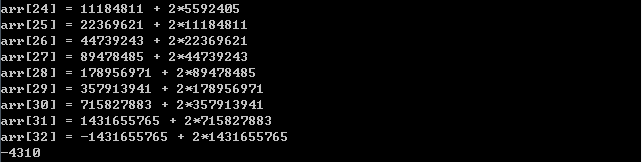
틀렸습니다 관된 소스는 integer표현 가능한 숫자의 범위를 벗어나서 숫자가 커질 경우 음수의 결과 값을 받게 되는 일이 발생하였다. 문제의 흰트에서 볼 수 있다 시피 10007를 괜히 나누는 것이 아니였다. 10007를 나눔으로써 2*1000까지의 타일을 구할 수 있게 된다. 
(arr[i] %=10007;를 for문 안에서 해주지 않고 마지막 cout 하는 부분에서 해주어서 틀렸음.)

n이 3일 경우

n이 8일 경우

n이 32일 경우
integer 표현 가능한 범위 : –2,147,483,648 ~ 2,147,483,647

arr[31] = 1,431,655,765 + 2 * 715,827,883 을 계산해보면 2,863,311,531로 integer표현 가능범위인 2,147,483,647을 넘게된다.

4. 문제

백준 알고리즘 : https://www.acmicpc.net/problem/11727

5. 틀린 문제

아래 답안은 시간 초과된 소스이다. 더 간단한 로직이 있는데 뻘짓을 했다. 기록용으로 남겨둔다.. ...

#include <iostream> #include <vector> #include <algorithm> #include <math.h> using namespace std; int main(){ int n; int numOfOne=0; int sum=0; int sizeOfvector; int numOfPermutation; int i; cin >> n; for (i=0; i<=n/2; i++){ numOfOne = n - 2*i; numOfPermutation = 0; sizeOfvector = numOfOne + i; vector <int>v(sizeOfvector,2); for(int j=0; j<numOfOne; j++){ v[j] = 1; } // next permutation do{ numOfPermutation++; }while(next_permutation(v.begin(), v.end())); sum += (pow(2,i) * numOfPermutation); } cout<<sum%10007<<endl; return 0; }

2*n 은 2*1, 2*2 두가지 경우가 있으므로 우선 한가지 경우만 순열을 구한 다음 각각 2*n 블록의 개수의 가짓수가 2개이므로 2의 n승을 해주었다. 
즉, 타일이 2*3일 경우, 
1) 11 11 11
2) 11 11 2
3) 11 2 2
4) 2 2 2 
와 같이 나눌 수 있는데, 이때 2에 해당하는 것을 
2) 11 11 (2*2) / 11 11 (2*1) : 2가지
3) 11 (2*2) (2*2) / 11 (2*1) (2*2) / 11 (2*2), (2*1) / 11 (2*1) (2*1) : 4가지 
4) (2*2) (2*2) (2*2) / (2*2) (2*2) (2*1) / (2*2) (2*1) (2*2) / (2*1) (2*2) (2*2) / (2*2) (2*1) (2*1) / (2*1) (2*2) (2*1) / (2*1) (2*1) (2*2) / (2*1) (2*1) (2*1)  : 8가지
위와 같이 2는 각각 2개의 경우의 수가 있으므로 2^n(2의 개수) 만큼 경우가 생긴다. 
이러한 로직으로 구현했는데.. 쓸데없는 짓이었다.
pow(2,i)가 시간 복잡도를 늘려서 시간 초과가 나왔다.

#include <iostream> #include <vector> #include <algorithm> using namespace std; int main() { int n; int numOfOne = 0; int sizeOfVector; int numOfPermutation=0; int i; cin >> n; for (i = 0; i <= n / 2; i++) { numOfOne = n - 2 * i; //numOfPermutation = 0; sizeOfVector = numOfOne + i; vector <int>v(sizeOfVector, 2); vector <int>tmpV(sizeOfVector); for (int j = 0; j<numOfOne; j++) { v[j] = 1; } // next permutation do { numOfPermutation++; } while (next_permutation(v.begin(), v.end())); std::copy(v.begin(), v.end(), tmpV.begin()); for (int j = sizeOfVector-1; j >= numOfOne; j--) { tmpV[j] = 3; do { numOfPermutation++; } while (next_permutation(tmpV.begin(), tmpV.end())); } } cout << numOfPermutation % 10007 << endl; return 0; }

위와 거의 같은 방법이긴 한데 
2의 n승을 없애고 2->3치환 후 전체 순열 개수를 구하는 로직으로 바꾸었으나 마찬가지로 시간 초과로 실패
(2는 2*1 , 3은 2*2 라고 생각하고 순열을 구해서 순열 개수로 구했음
마찬가지로 쓸데 없는 짓..

1) 11 11 11
2) 11 11 2
3) 11 2 2
4) 2 2 2 

2) 11 11 11 2 / 11 11 3
3) 11 2 2 / 11 2 3 / 11 3 2 / 11 3 3 
4) 2 2 2 / 2 2 3 / 2 3 2 / 3 2 2 / 2 3 3 / 3 2 3 / 3 3 2 / 3 3 3